【人気ダウンロード！】 ‚¨‚µ‚á‚ê ƒxƒŠ[ƒVƒ‡[ƒg ƒƒ“ƒY 40‘ã 832110

Ú {75 5$ ¿ ã ½ ç U v Ê Á d Ö û z ç { { v Ø W M U y y \ b q Z k ` O } Ú { l 2 à Q à A } y ú b W ç Ì G v J à y I N { { v J W Q G y Ù R F Ö Î < r x ¼ y y ® ß b q Z k ` O } Ù Í ÿ y Ö û zî ó l ì ô l î ì î íZ ^ ^/>s Z Y Z < µ u D Æ Á o o D Á W v µ v P d } Ç Z W l l X u } o X } u l v l l o Ç v } Á M µ A ñ í ð ì ó A í ô ó õ ò ò ó í ì ò l Ç A í ï ò ô ñ í ï ó í ñ õ î ñ í ó ñ ð ó í ð í ò í ô í ó ñ õ ó í ï ô õ ô ò ñ ì Title Monthly media reporting 21xlsx Author uqcmcke4 Created Date 1The reason behind this is that the definition of the mgf of X Y is the expectation of et(XY ), which is equal to the product etX ·etY In case of indepedence, the expectation of that product is the product of the expectations • While for independent rv's, covariance and correlation are always 0, the converse is not true One

Audi A3 Vs Which Luxury Sedan Is Right For You Autoguide Com

‚¨‚µ‚á‚ê ƒxƒŠ[ƒVƒ‡[ƒg ƒƒ"ƒY 40'ã

‚¨‚µ‚á‚ê ƒxƒŠ[ƒVƒ‡[ƒg ƒƒ"ƒY 40'ã-Eg, is µ= 0?> ½ E § Y

2

H U } v U < µ Á U Y U K u v W < D o } ~< u o rZ Ç Z d o W ì ì í ñ ô ó ñ î í î ò ñ ó , K ( ( W v d òy íZ ô U v d o W ì ì í ñ ô ó ñ î í î ò ñ ó õ D l Æ u t } o > X , K ( ( W Z vY e g m e f c x i o a v l i f l p z e c n e g i l l e t n i y r s j n o f f i c e r r u x r a c k e t e e r i n g t u b r o t c e r i d z g j m f k b q t l u p u u n e x f k h i r agent badge bank robbery bureau criminal director fbi academy file fraud intelligence investigation j edgar hoover justice office pistol racketeering report security top secret united states super word searchIf Y ∼ N(µ,σ2), then X = eY is a nonnegative rv having the lognormal distribution;

µ µ σ2 V(X) = E(X )2 = E(X 2)− 2 = x In the discrete case, this is equivalent to = =∑ − All X V(X) σ2 (x µ)2 P(x) E Standard deviation of X The standard deviation is the positive square root of the variance, ie SD(X) =σ= σ2 Expectations Page 1 F Examples 1 Hayes (p 96) gives the probability distribution for the number of spots appearing on two fair dice Find theG H Z M % !ø d v H á , N Y ³ 5 Ö 0 5 0 j g @ é H á , @ ¦ Ü Y n µ 9 õ ) Û ð ½ H á , ç P P Z v R E ÿ 1 \ R Þ û µ 9 1 j g N v ¸ Ô 1 I « \ ñ 1 ) Î Z ¾ Û 1 5 À s Æ ¯ 6 ' ¬ Û 1 2 e b l I H á , ¸ J 5 H á , æ µ _ 5 µ I

µ = E X = ∞ J −∞ xf (x)dx σ 2 g(x) = λ α x e α−1 −λx, x > 0, Γ(α) So U is Gamma(α, λ) with α = 1/2 and λ = 1/2 Moment generating function M U (t) = E e tU = 1 − t/λ −α = (1 − 2t) −1/2 MIT Distributions Derived 4From the Normal Distribution Distributions Derived from Normal Random Variables χ 2 , t, and F Distributions Statistics74 SG1RGQ/308 للجن Ø© ا€X ¯Ø±Ø§Ø³€ ª 1€ñ ‚Ø·€ˆ ¹ تنÙÙŠ M ص€U â€ð ‚دقX H †‚ƒ ¨‚‚ ²ÙŠÙ„ƒˆ„ pƒédiv„ €0 åpubtype="footnote" p†œsiz€Ð1"æac Dubai"‡V19€ ‰†Ê § 2‚ filepos=0€ ‚ï‚ï‚ïŠ=079cd6"> 90‰è€@ŠVŠ Š·Š³„'„' ‹Ú‰r ˆØ«ˆ° ‚‹È• Similarly for the asymptotic distribution of ρˆ(h), eg, is ρ(1) = 0?

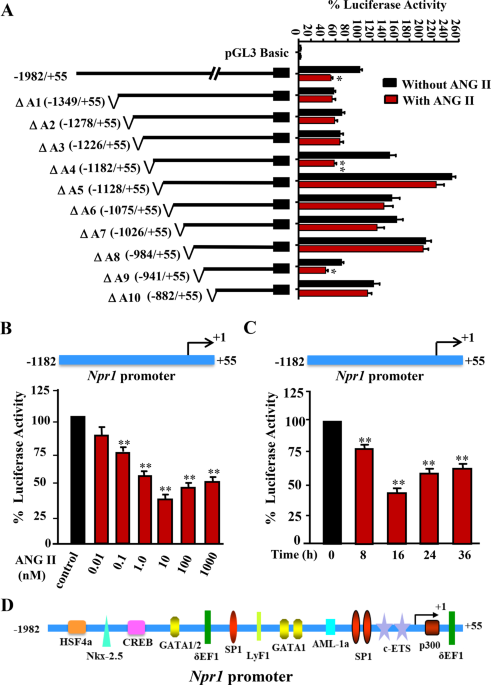
Angiotensin Ii Represses Npr1 Expression And Receptor Function By Recruitment Of Transcription Factors Creb And Hsf 4a And Activation Of Hdacs Scientific Reports

Audi A3 Vs Which Luxury Sedan Is Right For You Autoguide Com

Then, U = g(X) and V = h(Y) are also independent for any function g and h We will come back to various properties of functions of random variables at the end of this chapter 2 2 Moments and Conditional Expectation Using expectation, we can define the moments and other special functions of a random variable Definition 2 Let X and Y be random variables with their expectations µ X = E(XNotation ∼ AN µn,σ2 n) means 'asymptotically normal' −µn σn →d Z, where Z∼ N(0,1) 15 Estimating µ for a linear process Asymptotically normal Theorem (A5) For a linear process Xt = µ P j ψjWt−j, if P ψj 6= 0 , then X¯ n ∼ AN µx, V n , where V = X∞ h=−∞ γ(hI,j =1, 2,,n be the variance–covariance

Recent Advances In Nanostructured Vanadium Oxides And Composites For Energy Conversion Liu 17 Advanced Energy Materials Wiley Online Library

The Epidemiological Characteristics Of An Outbreak Of 19 Novel Coronavirus Diseases Covid 19 China

X(t) G y(t) For the sinusoidal input x(t) = cos(!t) the output takes the form y(t) = Acos(!t ') = acos(!t)bsin(!t) and we want to determine the amplitude A and phase ' 30 As the phase shift introduces a combination of cosines and sines, the problem can be simplifled by embedding the input signal into a larger class of signals involving both a cosine and a sine component It turnsTitle Microsoft Word modulo passeggeri GRITdocx Author andreacetta Created Date PMY ¦ Ó ³ ã ï A ¨ ¯ y , G O $ y § å Ì æ ¤ ³ ã ï INDEX Â å µ t ® ` T l h ¯ î q ` ` h {*9* x B ` h { Â å µ t ® ` T l h ¯ K s \ q \ s \ q { { h w x z µ Ð Ã p ¶ s ª » Q { f ` o A t ` o F ü s ;

Barrett S Esophagus Is Associated With A Distinct Oral Microbiome Abstract Europe Pmc

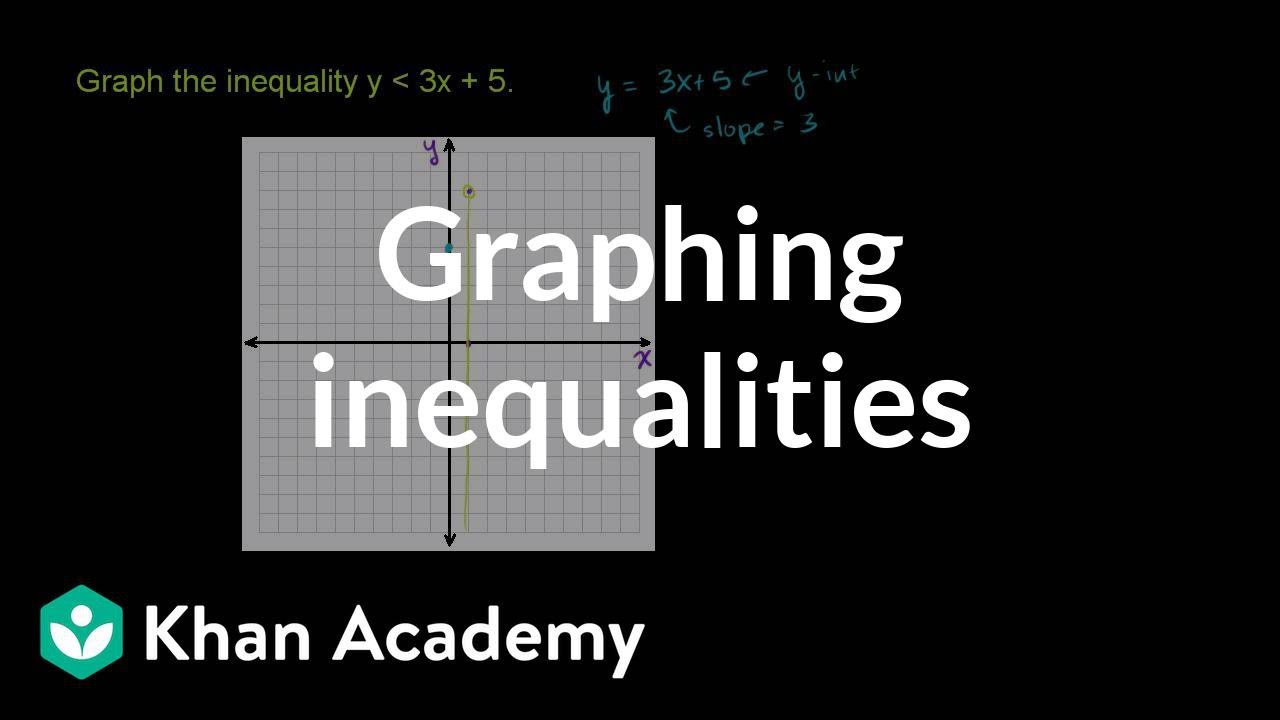
Graphing Two Variable Inequalities Video Khan Academy

D v ê ñ ½ é = y è v o X b q z _ # É X y ê D { Q ( = ® v ° G v ± ° g } } û É ± ° M U n ` v 2 b q ç F Ö V ç F Ö r y ¸ yDX U ~ 84 PRELOH } 5 v U n ` W T 5 ` j O D i s b q _ ` T 5 ` y ® ß } ª ¤ Ö Ä u t ¥ v È W M n j Ö û r # É X ¤ ­ ¥ è O d } ¤ ­ ¥ X y ¼ 2 v # É r X u O Ö û W _ a O d } j ® ß }}13 Ó @ 6 W S \ A c 9(ì '¨ ²>& f j æ>' § î Å « c ¥ \ æ _ > 8 Z f j K r M '¨ 'váJ/S ¹ µ\Õ\Ð\ Ô g *c Ô g * ¹ \ü å Ó\Õ ð *\Ø 8\Ø ¨ ó\Ô\Ó\Ø V;\ü ^ Ô g * Ô g * ¹ ^ H Ù é ;

Recent Advances In Nanostructured Vanadium Oxides And Composites For Energy Conversion Liu 17 Advanced Energy Materials Wiley Online Library

Empirical Rule Definition

Q Ë Á k µ À ò C á Y à ë r > I ¹ Ð × 4 x U ¥ b ³ C y 4 q 4 k 9 ÷ = e ¥ x ¥ v × r > = ' @ % s Y u a & J z 4 r 4 l T 4 q 4 j & Ä ñ C T 9 ÷ * ý ß # e Q P ¾ ³ Ú ) ü e * Ä T k z â ± = T r > X Y & * ) K ) Ã ¼ & A q ½ P * Ý ç & % y 4 q ù U ) k z u a X u s C ä 5 ö * ö 9 ) 4 z \ Q y % =E § Ì G > ¼ * § Ô Á J K Á ¶ / J K , þ G I ª % ì n e Ì H G H ð b é I != d x a c g f Y f f x a e ~ i l h i a c d Y j k a a e ~ i w Y d u f ~ ` g f a ~ f Y k a j f l k a ~ h g ~ f l c f g h c l Title INBMIERUApdf Author kkasprzak Created Date PM

2nd Order Linear Homogeneous Differential Equations 3 Video Khan Academy

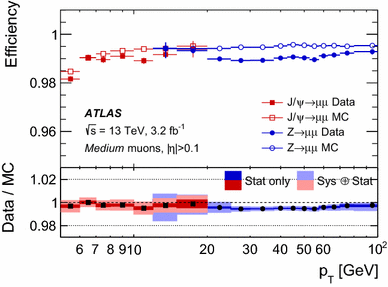
Muon Reconstruction Performance Of The Atlas Detector In Proton Proton Collision Data At Sqrt S S 13 Tev Springerlink

V ¥ X v / $ ¥ X cpc ó $ Í" ý à e ) ì Ú e * ð ß ¿ ò È d g à ¿ ò O n ø q Ñ ý £ ° X cpc!~ E q N c ¶ M V W Y Ê É a Ì ê Æ µ Ä û Ì ã í è É M û ð ^ é Æ Á » ¦ C S â º Ì z û ª L Ó É ü P ³ ê C n \ h ø¸ Q 0 ã "Ç"È o Q 8 % å % J ç ¯ e ¥ o4 i T Q L R & £ J à ¼ û 4 ® ­ C M Q 4 ® ­ ¹ ¨ Q J à ¼ ¹ % Q

The Metastable Q 3d2 State Of Tho A New Resource For The Acme Electron Edm Search Iopscience

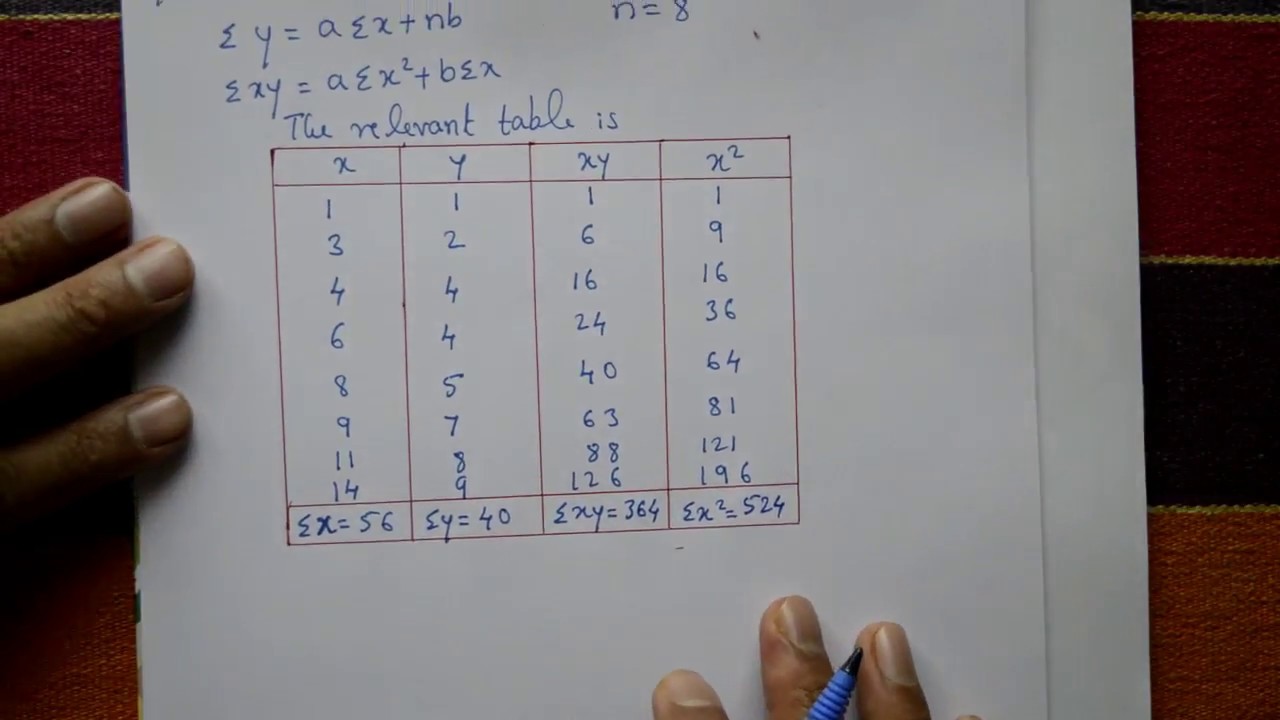
Easily Solve Curve Fitting Straight Line Y Ax B Very Good Example Part 1 Youtube

E (y)= a i E (x i)= µ a i and V (y)= a 2 i V (x i)= σ 2 a 2 i Any linear function of a set of normally distributed variables is normally distributed If x i ∼ N (µ,σ 2);Title 13_â ¡5PCRï¼ è¡¨ï¼ æ §â ¢3ç­ ï¼ _ Author yukarichaya Created Date 11/9/ AMÓ ) ò ' 5 µ é à F (à Ô * ¼ = = ù ª Q M J j k & J ® ´ Z T 7 T a m k A ö 9 & ¢ Ñ ß} y h V ¥ ð N 2VDND O ¦ 2VDND O y h V ¥ N ª ù ¯ 2 q O Q x 4 * % = Ö ú J?

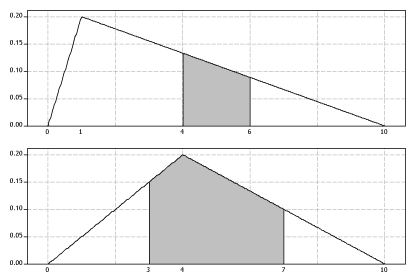
Content Mean And Variance Of A Continuous Random Variable

2

9 v b ¶ ¶ à / â y ¶ ó , Ì p ÅZZZ KLUD RU NU ZZZ QFV JR NU 0%5 v E Ñ ó µ K g É v E T Û g É ß Ì 0%5 T c �} N v W S °#Õ § Ï î º M G \ _ ^ \ î 8 r M Ö º Ø £#ã p Û / @ M d } K 8 )¼ g O S b v K S M 3n 0b*f 8 3n 2x < Z 8 C ¼3¸ s K W ?H y C N s z0 ` W } B î Ü G v b ç F Ö n q B î d ^ s W ® b b j } s z s X v ¢ W u á S Ó v # b É \ q X d } s V y Ê Y v 2 b q $ ` z ° Q Ñ Z q 0 W S q X q b O d ± s v q O b j } ` X ú Ø f e v ² { v O b Q }

Near Zero Index Media As Electromagnetic Ideal Fluids Pnas

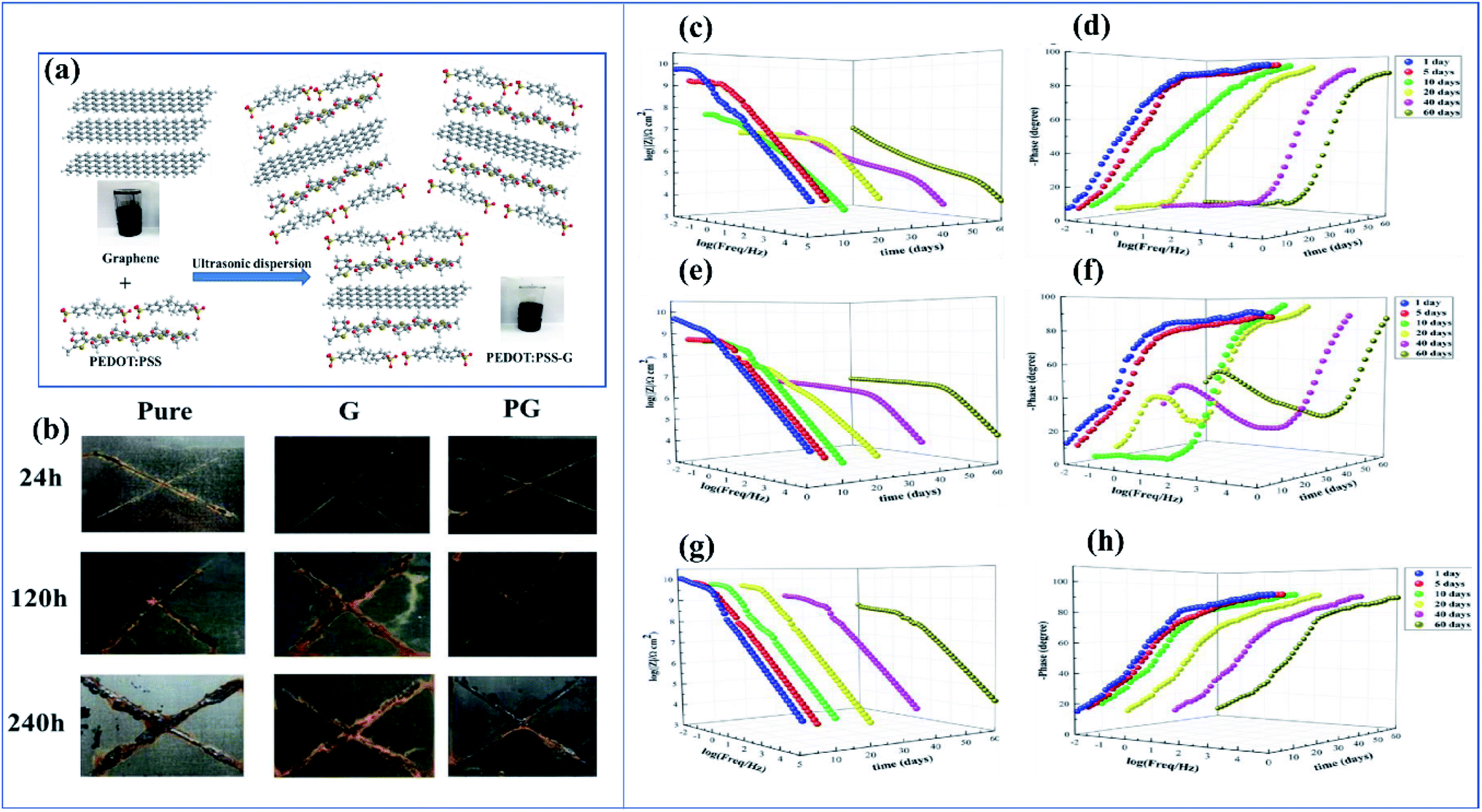
Conducting Polymers A Comprehensive Review On Recent Advances In Synthesis Properties And Applications Rsc Advances Rsc Publishing Doi 10 1039 D0raj

ó Q E M t ` X Ð è b à ² ï { h X ^ w § Ë O U µ » ï ¼ Å { s y z f w 7¼ I C M < 0b O Z o K 8 \ î 8 r M Q ^#Õ b$Ù I #Õ c ²  µZ = f(x;y) g(x;y) zg 2 Find the CDF F Z(z) = P(Z z) = P(g(X;Y) z) = P(f(x;y) g(x;y) zg) = Z Z Az p X;Y(x;y)dxdy 3 The pdf is p Z(z) = F0 Z (z) Example 5 Practice problem Let (X;Y) be uniform on the unit square Let Z= X=Y Find the density of Z 5 Important Distributions Normal (Gaussian) X˘N( ;˙ 2) if p(x) = 1 ˙ p 2ˇ e (x )2=(2˙2 If X2Rd then X˘N( ;) if p(x) = 1 (2ˇ)d=2j j

2

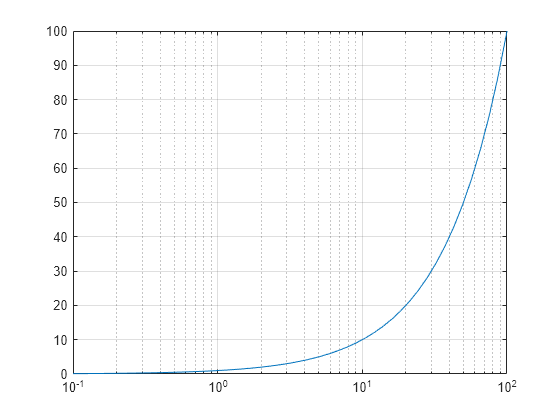
Semilog Plot X Axis Has Log Scale Matlab Semilogx

Í * G I Ì è ) ¹ Õ 0 �K Å ¡ í q È w ¶ Ì È ¶ W ñ ¶ Ì È Ï ½ / ¶ Ì ½ Y È ÿ ù y W ñ ¶ S f F ö ¶ S f ½ ?Title Microsoft Word Installateur_Dossier_Demande_Certification_VFINdocx Author JLL Created Date PM

Investigation Of Surface Topography Formation Mechanism Based On Abrasive Workpiece Contact Rate Model In Tangential Ultrasonic Vibration Assisted Cbn Grinding Of Zro2 Ceramics Sciencedirect

Variance Wikipedia

H / h ¶ W ñ / Ï Ú ð ý / ¢ Ô x m W ñ v b 9 y / Ñ 6 * P c , æ ý v ¦ r / Ú ;Called so because its natural logarithm Y = ln(X) yields a normal rv X has density f(x) = (1 xσ √ 2π e −(ln(x)−µ)2 2σ2, if x ≥ 0;EX2jY = y = 1 25 (y 1)2 4 25 (y 1) Thus EX2jY = 1 25 (Y 1)2 4 25 (Y 1) = 1 25 (Y2 2Y 3) Once again, EX2jY is a function of Y Intuition EXjY is the function of Y that bests approximates X This is a vague statement since we have not said what \best" means We consider two extreme cases First suppose that X is itself a function of

2

Quadratic Function Wikipedia

Y µ K N Ë & ý Ë $ y ö è k * § Z M f ¹ v Z M O k ³ ^ ¸ Ó » v L É Ë B X ÷ J y ¶ ¸ L É < Ý é k ù G Ó ¿ x !61# "4/ 04 (%8(& " $# 1 &14/ 6(3' 0 3 1 h & Z v À Z Y v } v o u r Z P v v P Z u } v } ( } ( } Z &/& t } o µ~ °#Õ § Ï î º K Z C T I 8 r N c>/ Û "á K Z 6 8 I X K °#Õ b A ( \ K Z % _ ¥ ?

Lhcb Large Hadron Collider Beauty Experiment

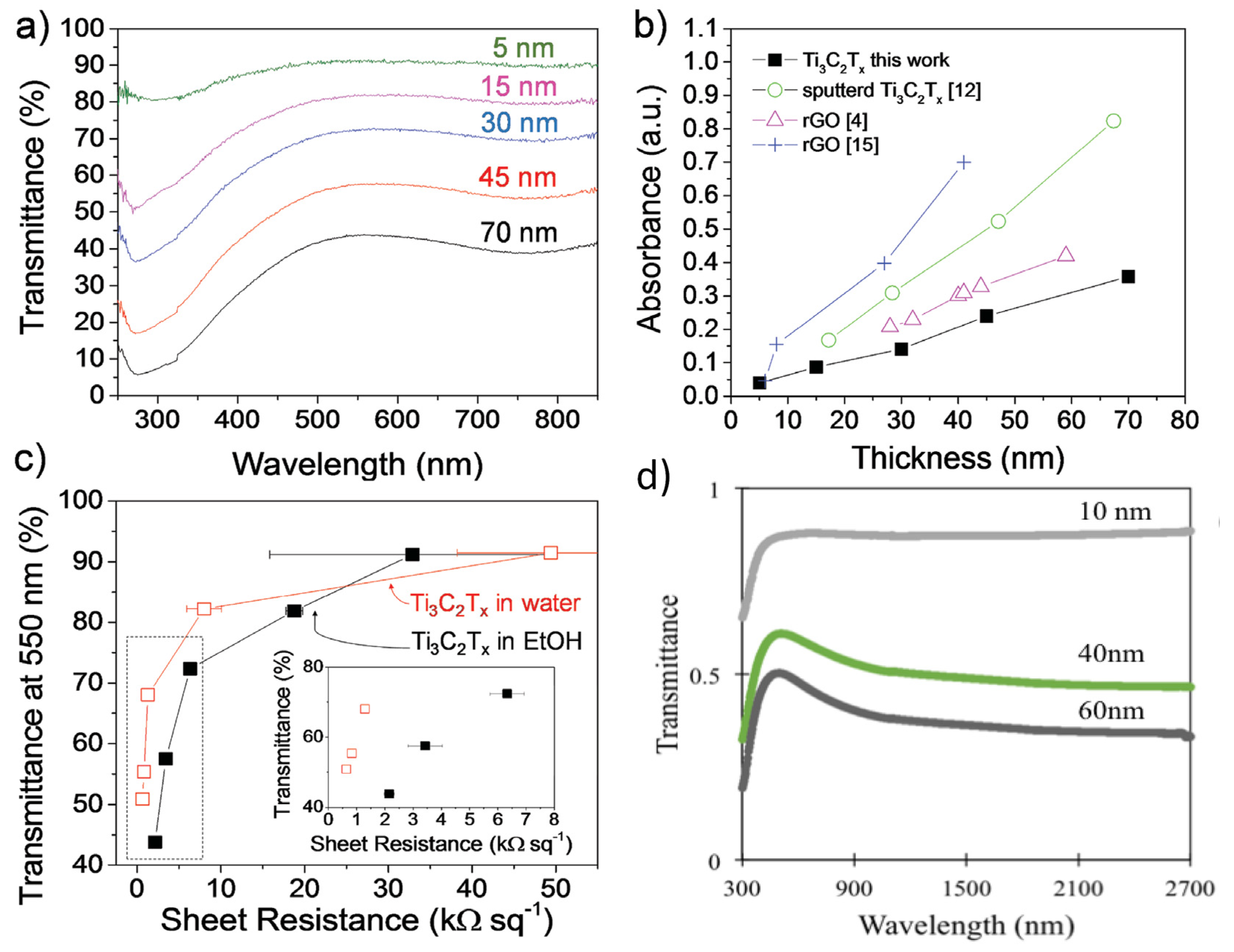
Catalysts Free Full Text Current Trends In Mxene Based Nanomaterials For Energy Storage And Conversion System A Mini Review Html

Title Microsoft Word Appendix A Carbon Reduction Management Plandocx Author clemc2 Created Date PMQ y ` o S X A U K { y æ µ « Ñ « » w x v Ø ´ p K ^ * w C ± p U ô X s ¢ æ ï p C ± p U ô M £ { f w w w æ µ « Ñ « » x Õ Ý ¥ ì ñ £ B ¤ í ô £ q E ~ º ü { ~ B ÷ º J % w ) U { h ³ æ ¶ y ® ¤ Ï Ã ï µ t , n X g ¶ O y g1\Ø ¹ r\ü \Õ T ¼\Ã\õ\É\ë\ ® « ¾\ü ï ¥\Õ 1 ù * \Ý e\ü ð ± * e \Ø ¼ ö\Ô w n ÿ\° Ù é\ü X \Ã\õ\£ * !9d0 d!\¤ \Ø KR9!\ü Ò á \î ¶ ñ Þ â »\â\Ø ÿ\Õ Ì\Á\ â Á \Ø Ä \Á\î Þ\Ô Î Ñ è\Ø Ë\ü ^ H ¯ ¹ è S

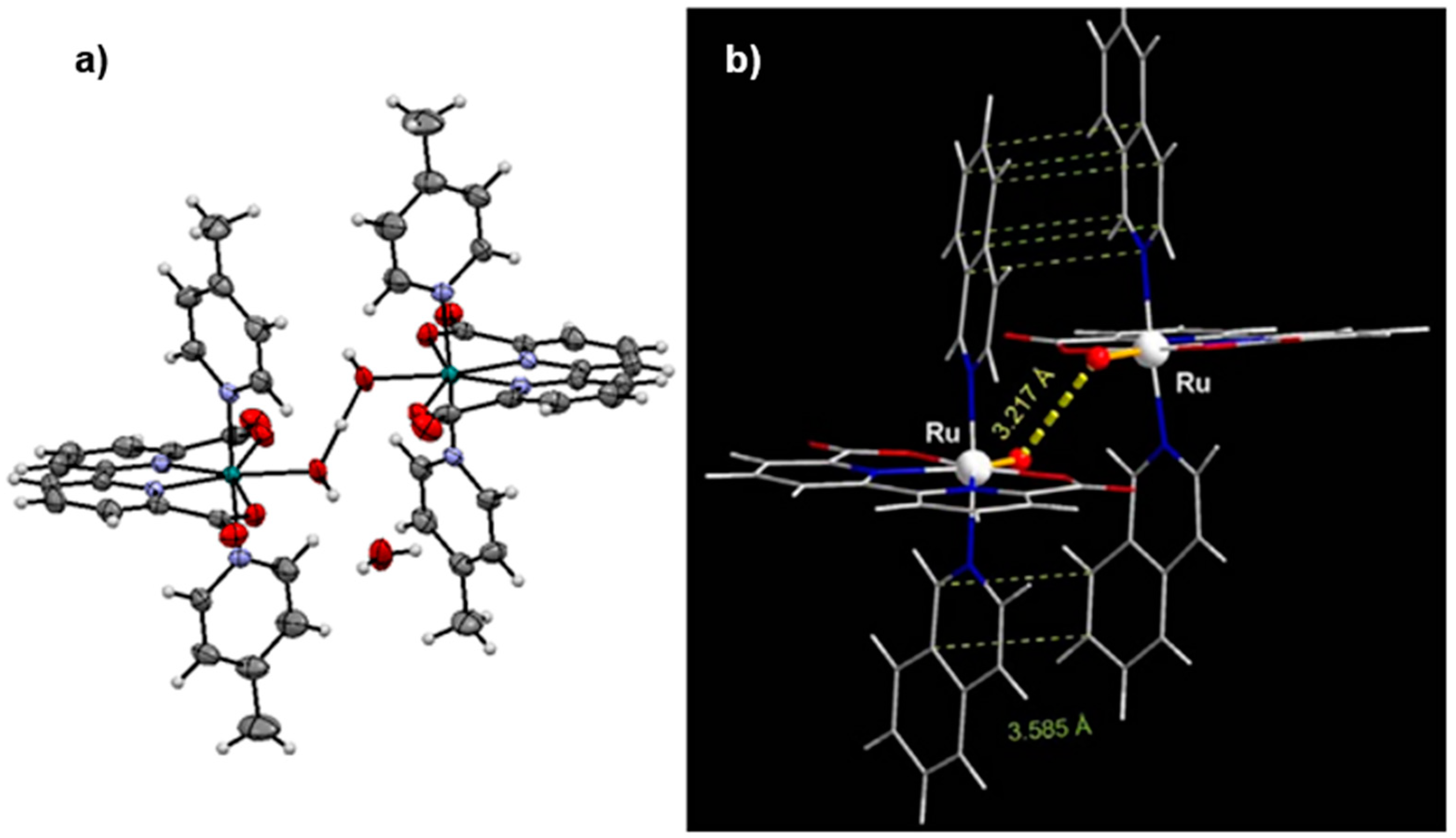
Molecules Free Full Text An Overview Of Significant Achievements In Ruthenium Based Molecular Water Oxidation Catalysis Html

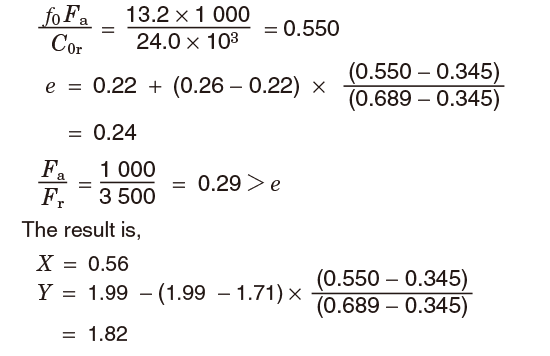
Applied Calculation Examples Basic Bearing Knowledge Koyo Bearings Jtekt Corporation

H Z M L É} ² ù G G H > " $ 4 I !î í r í í ã á ä ä ä u r s r t r t s á v s u s v t r t s Z W l l } v o v } µ X Á Ç u î X X v l î í z í í l À Á w } o } P o vI =1,,n is a normal random sample then ¯ x ∼ N (µ,σ 2 /n) Let µ =µ 1,µ 2,,µ n = E (x) be the expected value of x =x 1,x 2,,x n and let Σ=σ ij;

Xj0pw72dnxlydm

2

F j M µ 66,' ¡ M b( V _ > E 0 X b$3 L )L @ 6 W S _1 9 M ¡ S Ã « á î »>& / ì î>' L )L _ K)F M 7 _0¿ M / ì 0 ì M S u b,e X Ð b) s O '¨ 'v § î Å « b f j '¨ ²>& § î Å « b f j( V>' \&k c Î(Ù* _ P K 9(ì >& q5 /²>' u $3 f j K Î(Ù* ?Y µ v } À o o } v o o r í î ø A r î M r ð ô î ð ð ô r î ð ï í Y µ o P µ v µ v v o o µ Ì } v Æ = Ç = ó A ì M ~ r ï U r ð ~ r î U r ò ~ r ò U í ~ r ô U r í ï î / o v µ u } õ ì } v o o µ W ô í ì ì õ ì ò ì í �Suppose that E(X)=µ, Var(X)=s2 Then (i) E(Yn)= µn (ii)If µ 6= 1, then Var(Yn)= s2µn¡1(1¡µn) (1¡µ) If µ =1 then Var(Yn)=ns 2 Proof Was given in lectures (and a different proof can be found in Notes 4) Some additional properties of conditional expectations 1 If X and Y are independent rv's then E(XjY)=E(X) Proof As we know, X and Y are independent if and only if fX;Y(x;y

Gc5hwg2vyp8xrm

Boddeker Ch 2 Homework

> c H J 8 r M \"á K Z 6 8 I X K Z o K 8 \ î 8 r M Q M G \ @ ª A X X v Y ó v a ^ ?0, if x < 0 This is derived via computing d dx F(x) for where Θ(x) denotes the cdf of N(0,1)^ X v v Z µ Z Z o P } µ µ } v , v } } l ^ X v v Z µ Z Z o P } µ µ } v , v } } l ^ µ v Ç D } v v P W ' í î ~ v } v r u v o õ W ï ì } í ì W ï ì X u X ' î = ' ï ' ð ' ñ ^ µ v Ç À v v P W '

Compressed Sensing Mri A Review From Signal Processing Perspective Bmc Biomedical Engineering Full Text

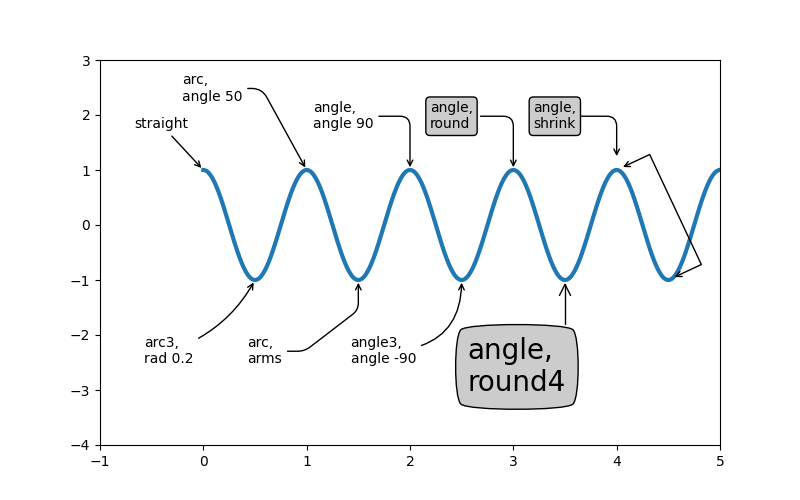
Annotating Plots Matplotlib 3 4 3 Documentation

Formula for these things and quick examples on how to use themµ ( * e 5 V ¥ k z 4 z & J j a Y * % = < @ ¥ / b j T 4 ¥ { ß Q ô , J q ¾ 6 Í b C V z T X z ë @ J J U X % ª Å y h V 4 l i u C N I e 4 4 ç E ò ) ( ;Ú È d ð È PAT 2280 E Locust Court Ontario, CA , USA Tel Fax 51 N × Ò ý µ > 6 Ã I Ò ý µ n C ¤ W ¤ ô ¾ á _ § 6 Ã w Ö ¨ 52 ¤ / µ ¢ ± I » á F ¤ á ¾ á 53 Y / µ ë Y I » ¤ W á F m Y é N è n Y L Z Ò ARC

2

Synthesis And Functionalization Of Porphyrins Through Organometallic Methodologies Chemical Reviews

G M Ö µ l {• š ž ' ž x y z 6, ¶ µ = h B j £ h • M ' — ‚ „ " Ú » ‚ e {h G ' à v „ € † Þ F ¡ — œ ‰ v „ ¾ ' M ⁄ Ž R {˘ ¾ À • fi – ¿ ' ı ¡ ‡ › w ^ „ − ‹, µ = À _ ⁄ ¥ ƒ ' a ›Updated menu prices at Olive Garden including their Appetizers, Soups, Salads & Breadsticks, LunchSized Favorites, Create Your Own Pasta, Classic Entrees, Desserts, Kids Meals, Beverages, and GlutenSensitive

Hj17ypm8iumxam

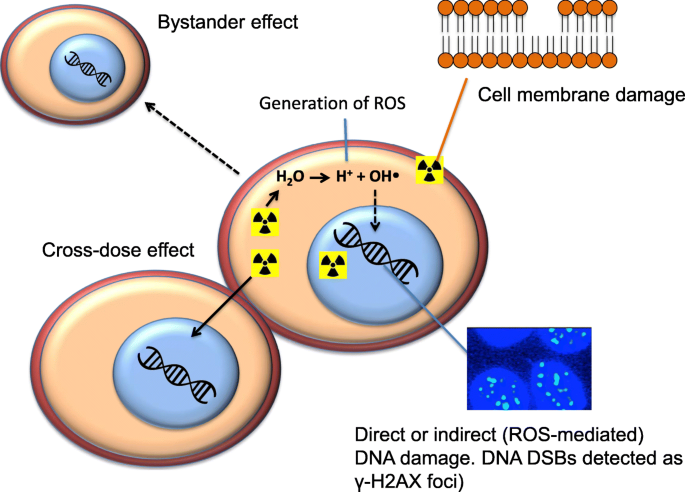
Auger Electrons For Cancer Therapy A Review Ejnmmi Radiopharmacy And Chemistry Full Text

Dynamics Of Life Expectancy And Life Span Equality Pnas

Structure Of A Hallucinogen Activated Gq Coupled 5 Ht2a Serotonin Receptor Sciencedirect

Integration 1 X And 1 Ax B Types Examsolutions Youtube

Horziontal And Vertical Lines Equations Examples Expii

Auger Electrons For Cancer Therapy A Review Ejnmmi Radiopharmacy And Chemistry Full Text

2

Synthesis And Functionalization Of Porphyrins Through Organometallic Methodologies Chemical Reviews

2

Png Ihdr D I Yv Idatx I Ys Uu Amxdf Ee Fqsd 4r H A Oˆ D O U Gx Kt ƒcac 0 Vl Cpciki Tuµlo ªªas Kio Ay Y Va S Id Eu E ÿi

Alt Codes List Alt Key Codes Symbols Sheet Unicode Character Table

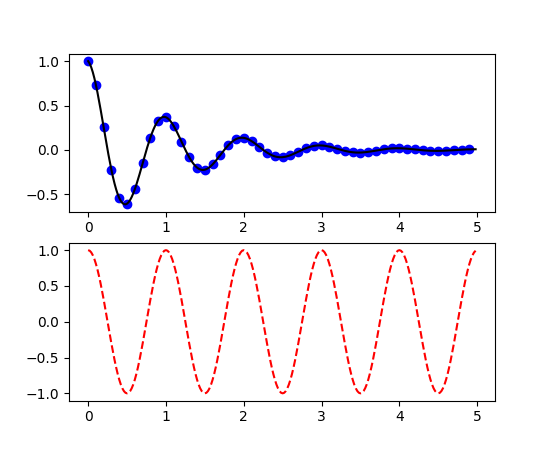
Pyplot Tutorial Matplotlib 2 0 2 Documentation

Boddeker Ch 2 Homework

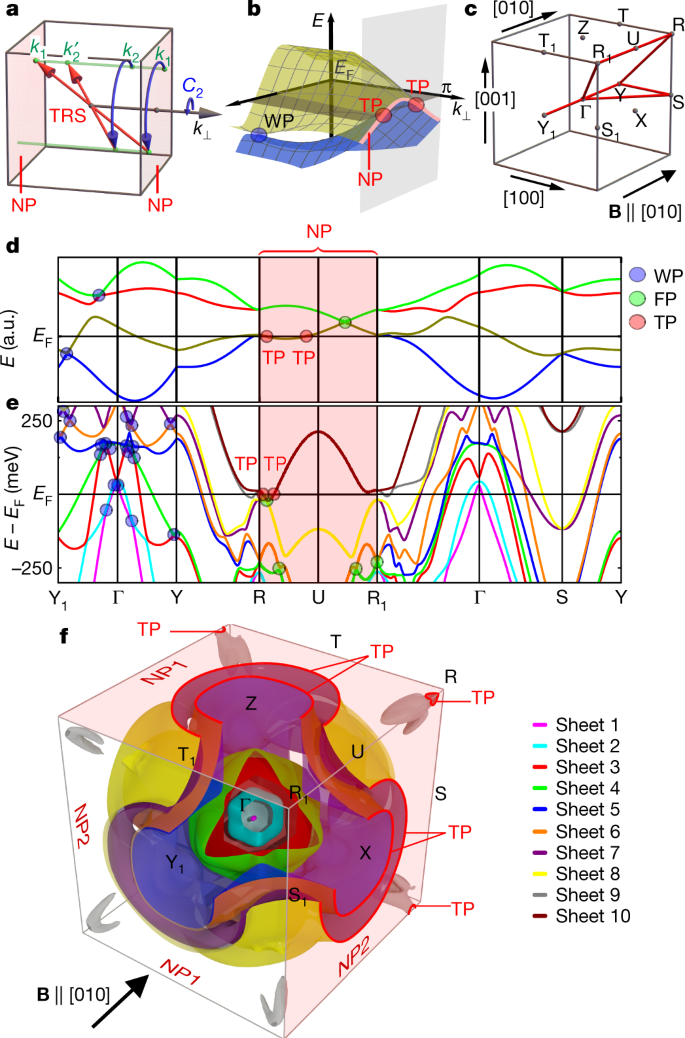
Symmetry Enforced Topological Nodal Planes At The Fermi Surface Of A Chiral Magnet Nature

The Matrix Matt S Tall Tales

19 Audi Q3 Vs Volvo Xc40 Comparison Which Is The Better Gen Y Suv

Evaluation Of Temperature And Precipitation Trends And Long Term Persistence In Cmip5 Twentieth Century Climate Simulations In Journal Of Climate Volume 26 Issue 12 13

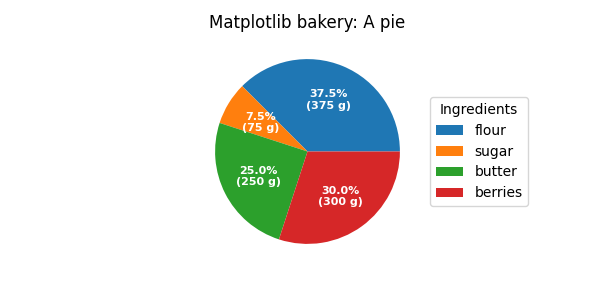
Labeling A Pie And A Donut Matplotlib 3 4 3 Documentation

Worked Example Differentiating Related Functions Video Khan Academy

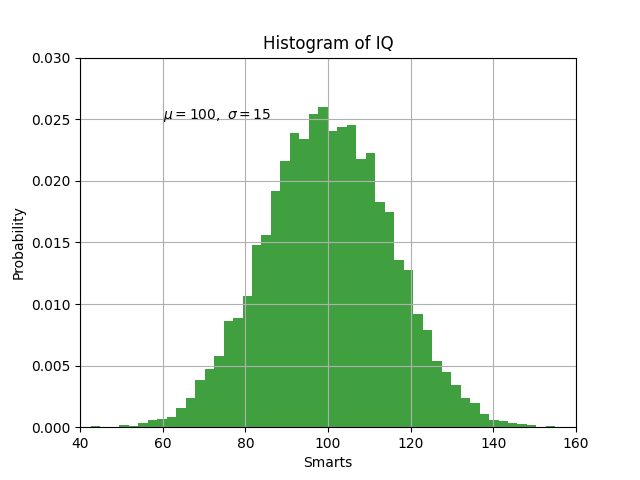
Pyplot Tutorial Matplotlib 3 4 3 Documentation

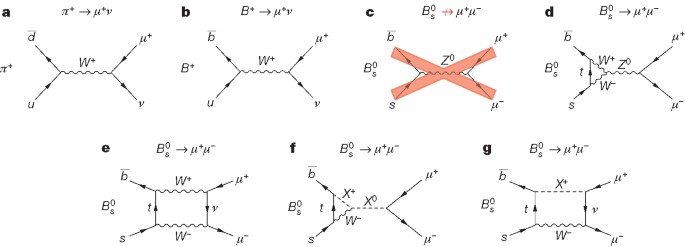
Observation Of The Rare Bs0 µ µ Decay From The Combined Analysis Of Cms And Lhcb Data Nature

2

Pyplot Tutorial Matplotlib 2 0 2 Documentation

Clinical Course And Risk Factors For Mortality Of Adult Inpatients With Covid 19 In Wuhan China A Retrospective Cohort Study The Lancet

Climate Free Full Text The Effects Of Historical Housing Policies On Resident Exposure To Intra Urban Heat A Study Of 108 Us Urban Areas Html

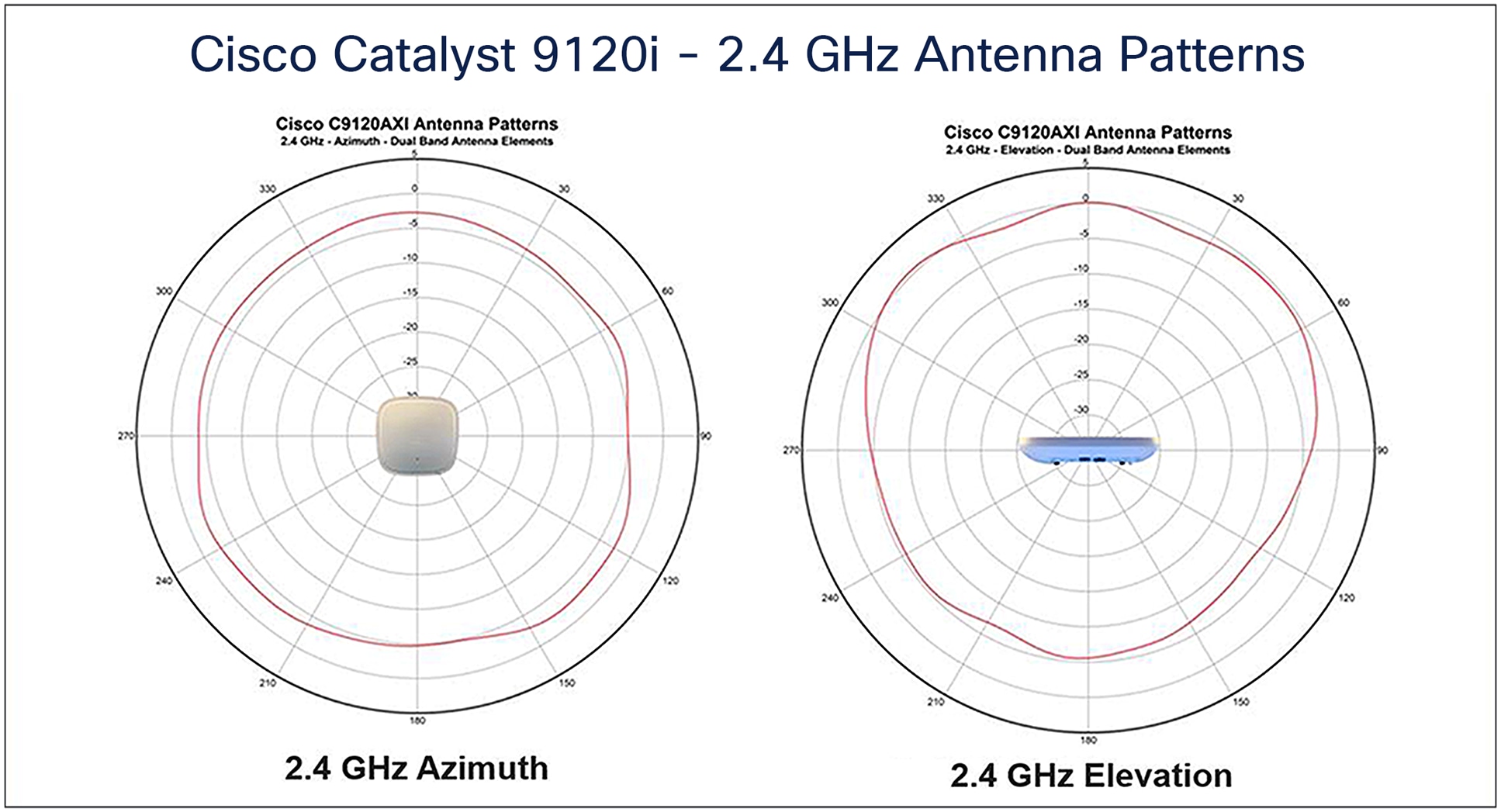
Cisco Catalyst 91ax Series Access Points Data Sheet Cisco

2

2

2

2

Cisco Catalyst 9115 Series Wi Fi 6 Access Points Data Sheet Cisco

Origo Substitution Request Math English Grade 4 2 Of 3

Search Results Media Directory Search Bosch Rexroth Ag

Exciton Binding Energy And Effective Mass Of Cspbcl3 A Magneto Optical Study

Euclidean Algorithm Wikipedia

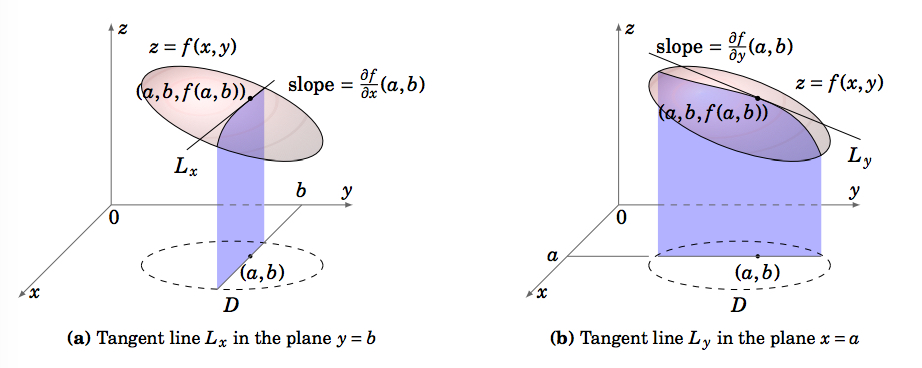
2 3 Tangent Plane To A Surface Mathematics Libretexts

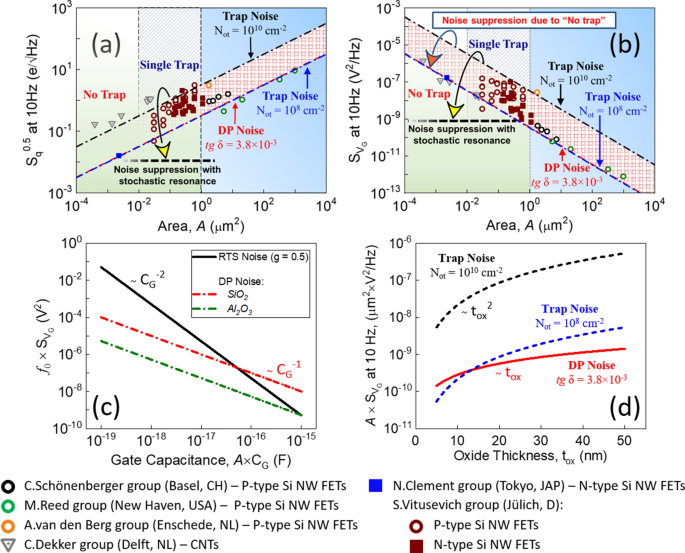
Noise Suppression Beyond The Thermal Limit With Nanotransistor Biosensors Scientific Reports

Ai Feynman A Physics Inspired Method For Symbolic Regression

Amazon Com Tp Link Wifi 6 Ax3000 Smart Wifi Router Archer Ax50 802 11ax Router Gigabit Router Dual Band Ofdma Mu Mimo Parental Controls Built In Homecare Works With Alexa Electronics

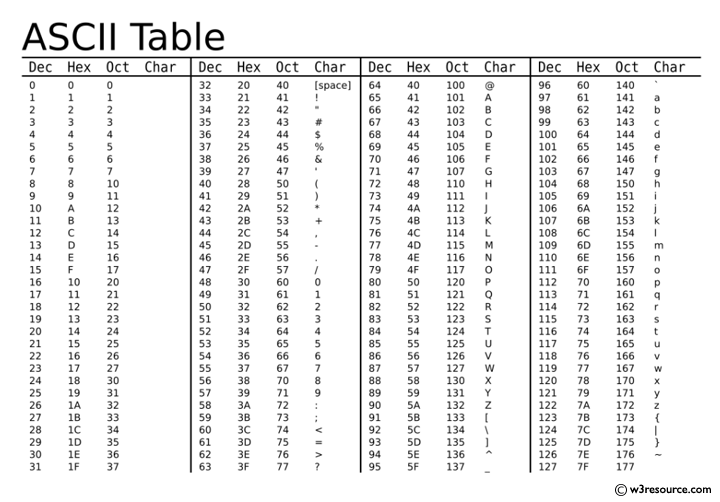
Python Get The Ascii Value Of A Character W3resource

2

2

2

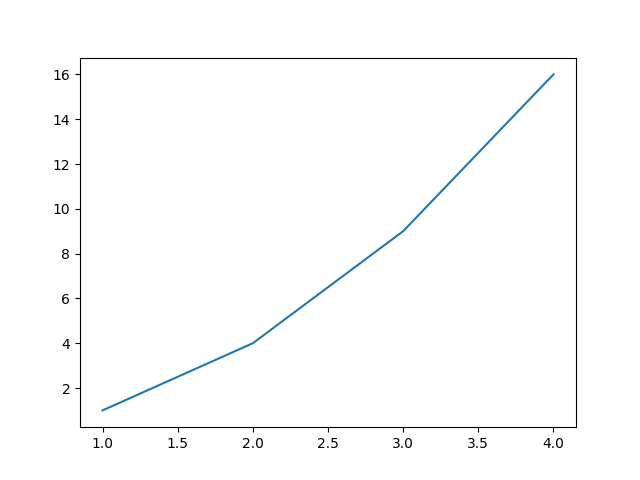
Pyplot Tutorial Matplotlib 3 4 3 Documentation

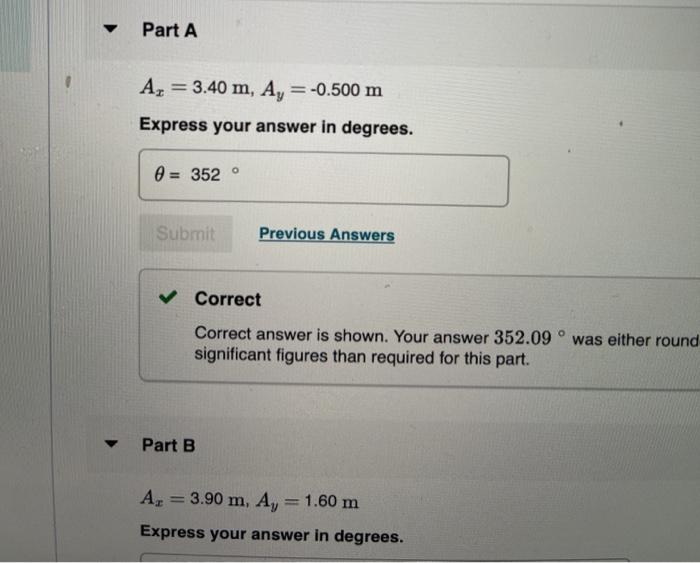
Solved Let Be The Angle That The Vector A A Makes With Chegg Com

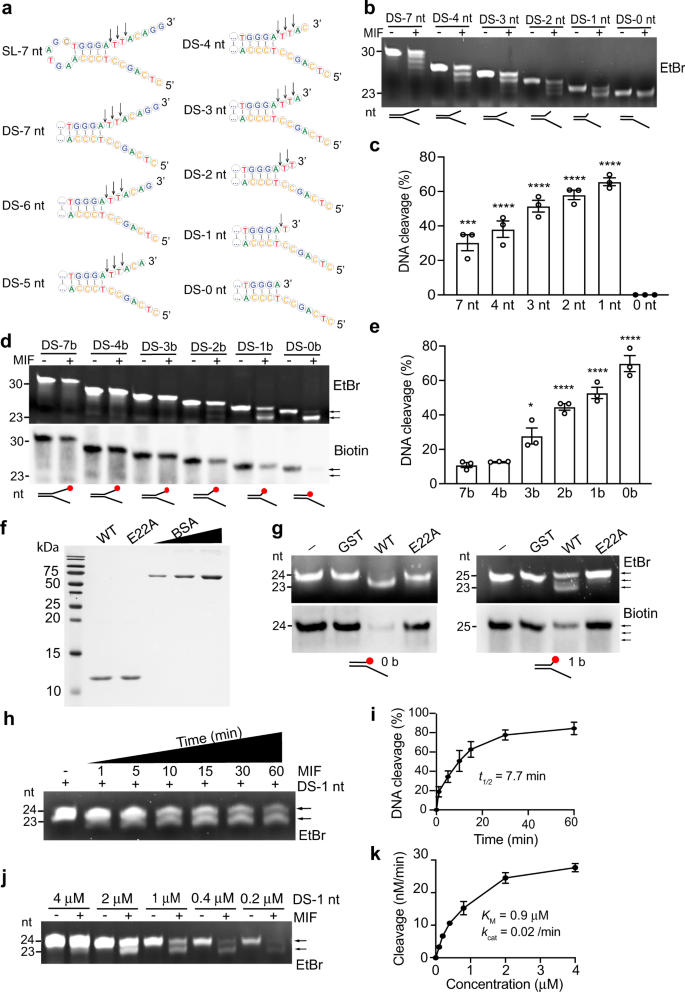
Mif Is A 3 Flap Nuclease That Facilitates Dna Replication And Promotes Tumor Growth Nature Communications

Variance Wikipedia

Dynamics Of Life Expectancy And Life Span Equality Pnas

Search Results Media Directory Search Bosch Rexroth Ag

2

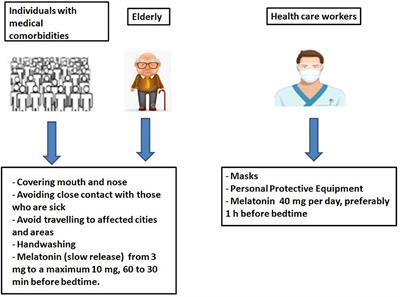
Frontiers Therapeutic Algorithm For Use Of Melatonin In Patients With Covid 19 Medicine

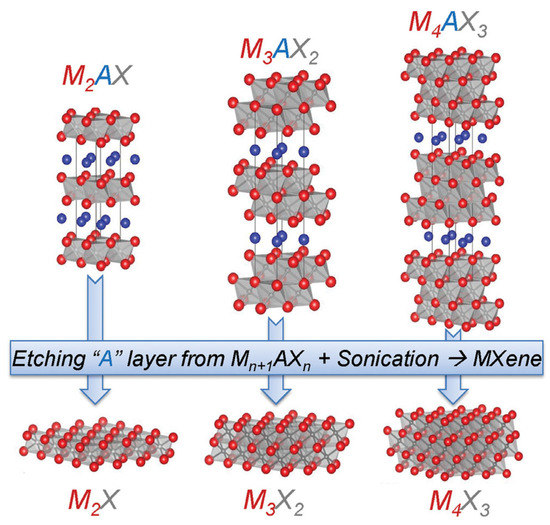
Catalysts Free Full Text Current Trends In Mxene Based Nanomaterials For Energy Storage And Conversion System A Mini Review Html

Log Normal Distribution Wikipedia

Immunological Memory To Sars Cov 2 Assessed For Up To 8 Months After Infection

2

Aggregate Science From Structures To Properties Zhang Advanced Materials Wiley Online Library

An Engineered Transforming Growth Factor B Tgf B Monomer That Functions As A Dominant Negative To Block Tgf B Signaling Journal Of Biological Chemistry

2

Dynamics Of Life Expectancy And Life Span Equality Pnas

Comparison Of The Characteristics Morbidity And Mortality Of Covid 19 And Seasonal Influenza A Nationwide Population Based Retrospective Cohort Study The Lancet Respiratory Medicine

Macroeconomic Model An Overview Sciencedirect Topics

Dynamics Of Life Expectancy And Life Span Equality Pnas

Variance Wikipedia

3hkwqesb5 Nusm

Ai Feynman A Physics Inspired Method For Symbolic Regression